Here’s an interesting concept, and one that’s, rather surprisingly, widely unknown. It’s called tetration, a concept brought up so rarely that most computer dictionaries don’t even recognize it as being a word. I was organizing my filesystem hierarchy today, and found this old paper I wrote for my Discrete Mathematics class. I gave it a quick re-read, and the concepts still amaze me. It is truly impossible to ignore the beauty of mathematics, especially after seeing something like this.
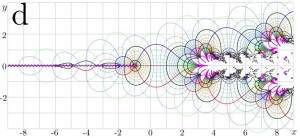
Drawing of the analytic extension f = F(x + iy) of tetration to the complex plane.
The basic premise of tetration is simply a continuation of what has already been examined since, well, probably kindergarten. Everyone knows what addition, subtraction, multiplication, and division are. But consider this concept for a moment: multiplication is just repeated addition, exponentiation (x^y) is just repeated multiplication, and tetration, well, that’s just repeated exponentiation! It has other names as well. Since it’s concept looks something like a^b^b^b^b, it has been called a power-tower. It is also interesting to note that we’ve all seen an equation somewhere or another that may have looked something like: a^b^2. Now, the simplest way to solve this would be to start by squaring b, then raising a to that power. But if b were to resolve to a value of two – well, that’s tetration! It’s pretty neat to see how tetration can be often be used, yet is relatively unknown.
And here’s where it starts to get even stickier – it doesn’t stop at tetration! If there’s an operation n, that means that there is an operation n+1 which formulates itself as the repeated nth operation. So that means there’s an infinite number of operations that can be performed on numbers. It’s also crazy to think that there’s an operation at infinity, so that given any non-zero inputs, an infinite value would be returned. There’s a lot of power to be found in tetration and nth-term iterative operators, and oddly enough, if I had to guess that the problem had a solution, I would say this would be a good starting point for which to solve the [Riemann hypothesis].This is some crazy stuff here, and if it’ll help anyone to further understand, I’ve uploaded my findings on tetration to this server for download [here]. Enjoy!